EP 123: ทำ Arbitrage ผ่าน Put-Call-Futures Parity

Futures

ครบเครื่องเรื่องสินค้าใน TFEX
EP 123: ทำ Arbitrage ผ่าน Put-Call-Futures Parity

โอกาสทำ Arbitrage จาก Options
ปัจจุบันการซื้อขาย Options ใน TFEX สภาพคล่องอาจจะยังไม่ได้สูงมากนัก จึงทำให้อาจเกิดความบิดเบือนของราคา (Mispricing) ซึ่งนักเทรดบางกลุ่มจะมองหาโอกาสนี้เพื่อค้ากำไรโดยปราศจากความเสี่ยง หรือที่เรียกว่า Arbitrage นั่นเอง วันนี้ทางทีม BLS Futures & Options จะพาทุกท่านไปรู้จักวิธีการค้ากำไรจาก Options กันครับ...

แนวคิด Put-Call-Futures Parity มาจากไหน

ก่อนอื่นเลยต้องมาทำความรู้จักกับแนวคิด Put-Call Parity กันก่อน โดยแนวคิดดังกล่าวเริ่มต้นมาจากนักเศรษฐศาสตร์ ชื่อ Hans R. Stoll ในปี 1969 ซึ่งเขาได้กล่าวถึงความสัมพันธ์ระหว่างมูลค่าของ Put และ Call options ที่มีสินค้าอ้างอิงตัวเดียวกัน มีราคาใช้สิทธิที่เท่ากัน และระยะเวลาหมดอายุที่เท่ากัน ต่อมามีการประยุกต์ใช้ Futures เข้ามาแทนสินค้าอ้างอิง จึงต้องใช้ Put-Call- Futures Parity จาก Alan L. Tucker ในปี 1991 โดยสามารถอธิบายความสัมพันธ์ได้โดยสมการต่อไปนี้

LHS RHS
C + K(1+R/365)^(-t) = P + F(1+R/365)^(-t)

โดย C = ราคา Call Options
K(1+R/365)^(-t) = มูลค่าปัจจุบันของราคาใช้สิทธิ
           F(1+R/365)^(-t) = มูลค่าปัจจุบันของ Futures
R = อัตราดอกเบี้ยปราศจากความเสี่ยง
           t = อายุคงเหลือของ Options (วัน)
P = ราคา Put Options
F = ราคาของ Futures

จากสมการข้างต้น Arbitrage จะเกิดขึ้นเมื่อข้างใดข้างหนึ่งของสมการมีค่าไม่เท่ากัน โดยนัก เทรดจะขายข้างที่แพงกว่า และซื้อข้างที่ถูกกว่าทันที ซึ่งจะได้กำไรโดยปราศจากความเสี่ยง

เมื่อพบ 2 ข้างสมการของ Put-Call-Futures Parity ไม่เท่ากัน

นักเทรดสามารถจัดกลยุทธ์ โดยการเข้าไปซื้อขาย options และ futures ถือไว้จนกระทั่งครบกำหนดอายุ

ตัวอย่าง สมมุติราคา S50Z23 มีมูลค่าปัจจุบัน 879.1 บาท Call options S50Z23C900 ที่จะถึงวันหมดอายุอีก 56 วัน ราคาใช้สิทธิ 900 บาท มีมูลค่า 12.2 บาท และ Put options S50Z23P900 มีมูลค่า 38.8 บาท อัตราดอกเบี้ยไร้ความเสี่ยงร้อยละ 2.31% ต่อปี
(ตัวอย่างดังกล่าวยังไม่รวมค่าธรรมเนียมต่าง ๆ)

LHS:
C + K(1+R/365)^(-t)
= 12.2 + 900[(1+(0.0231/365)]^(-56)
= 909.02

RHS:
P + F(1+R/365)^(-t)
= 38.8 + 879.1[(1+(0.0231/365)]^(-56)
= 914.79

จากสมการด้านบนจะเห็นว่า RHS หรือฝั่ง Put options มีมูลค่ามากกว่าฝั่ง LHS หรือ Call options ส่งผลให้เกิดโอกาสในการเข้าทำกำไรแบบปราศจากความเสี่ยง โดยการ Long Call options และ Short Put options และ Short S50Z23

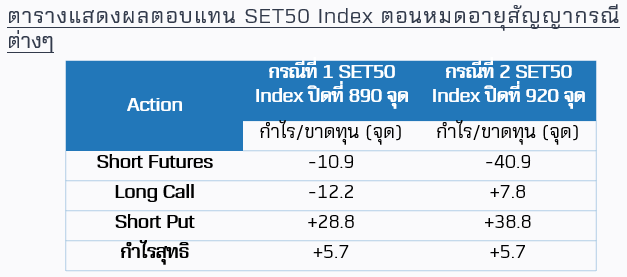
Arbitrage Profit Table .png

จากตัวอย่างข้างต้นพบว่าไม่ว่าในอนาคต SET50 Index ตอนหมดอายุสัญญาจะปรับขึ้นหรือลงไปที่เท่าไหร่ นักลงทุนจะได้กำไร 5.7 จุด เสมอ ซึ่งจะเห็นได้ว่าราคา Put กับ Call นั้นมีความสัมพันธ์กัน และถ้าเมื่อไหร่ก็ตามที่ไม่เป็นไปตามสูตรข้างต้น เราก็มีโอกาสที่จะทำ Arbitrage ได้

Source: BLS Futures and Options as of 03/11/23

😎👉🏻 สมัครเปิดบัญชี TFEX / Block Trade ผ่าน Wealth Connex คลิกที่นี่

☎ สอบถามข้อมูลเพิ่มเติมได้ที่ BLS Customer Service โทร 0-2618-1111

------------------------------------------------------------------------------